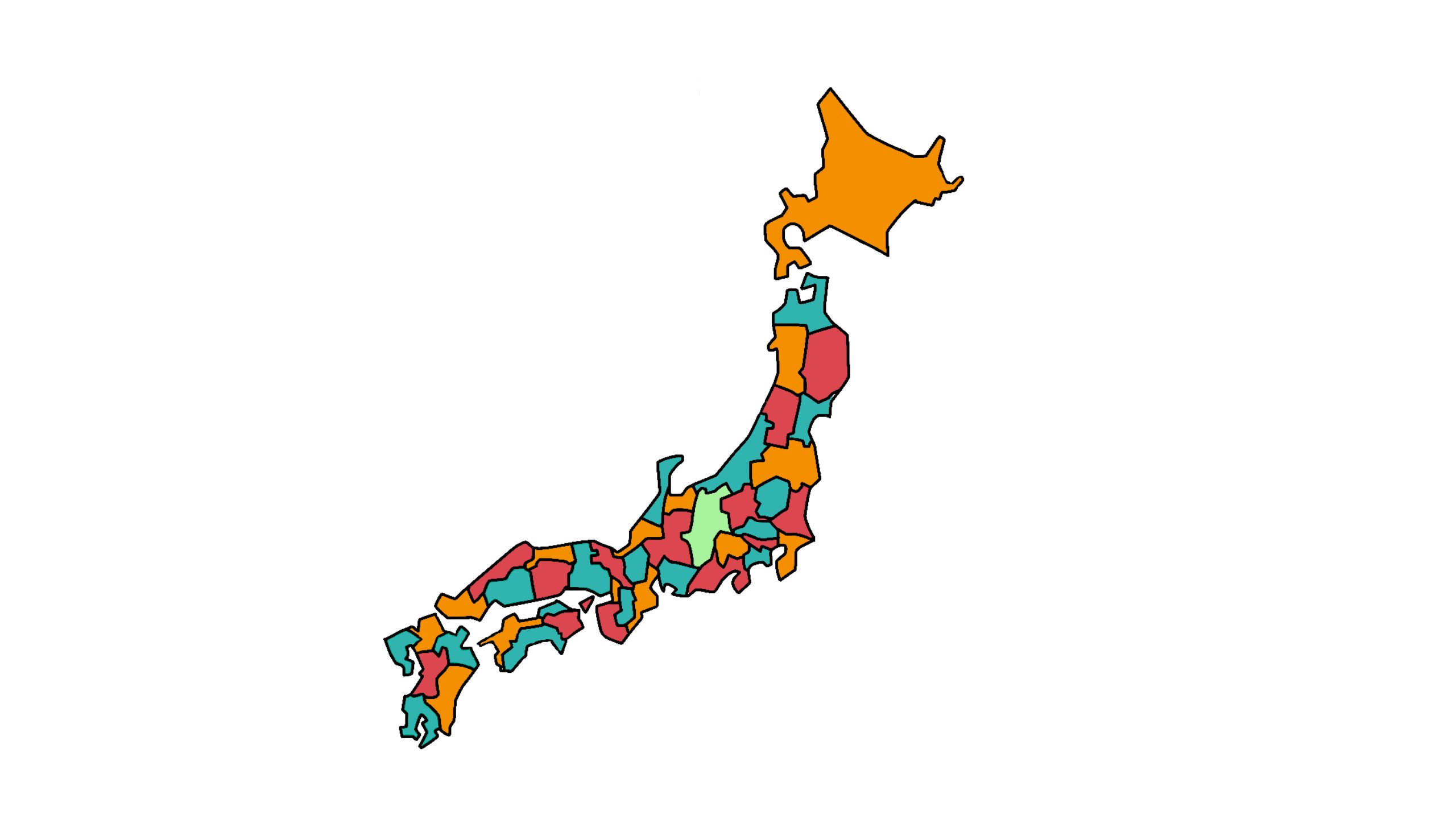
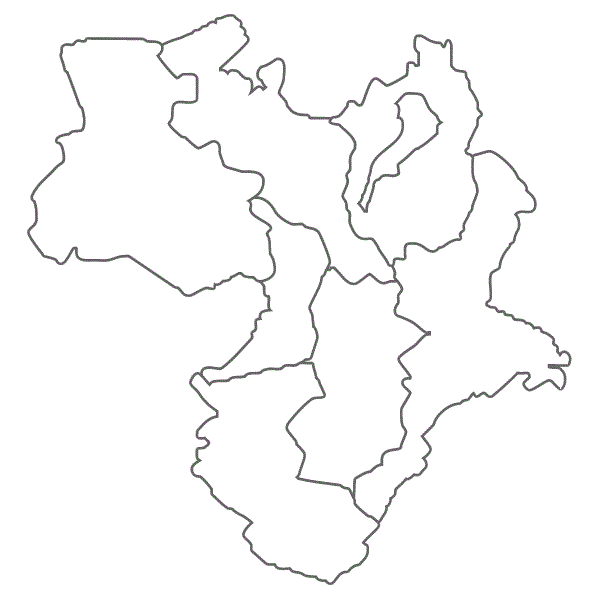
THE FOUR COLOUR THEOREM Robertsonらによる実際の633個の可約な不可避配置集合を見ることができる。 双対グラフ表記のため、国が頂点、国境が枝で表される。最初の配置はバーコフのダイヤモンドであり、黒丸が5枝点をあらわす。 以下、無印が6枝点、白丸が7枝点、四角が
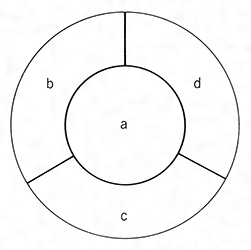
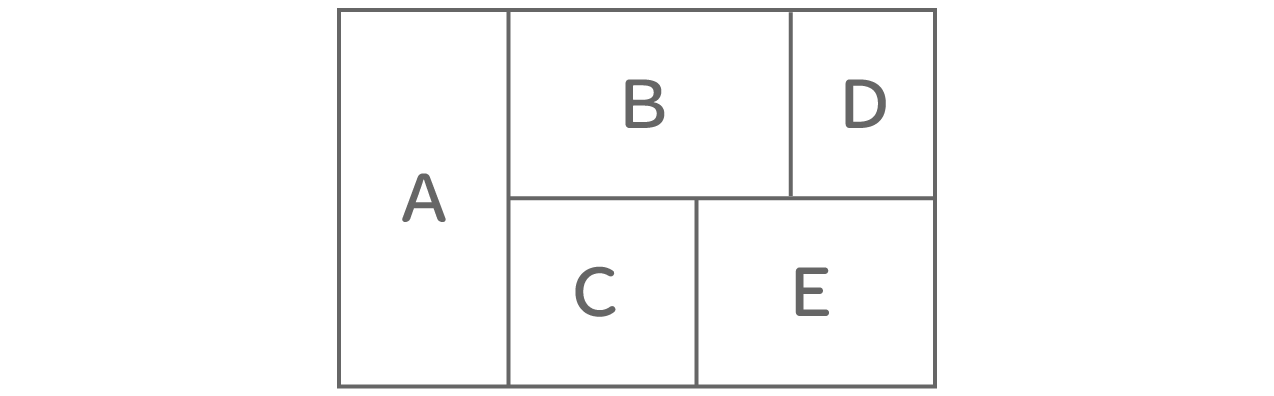
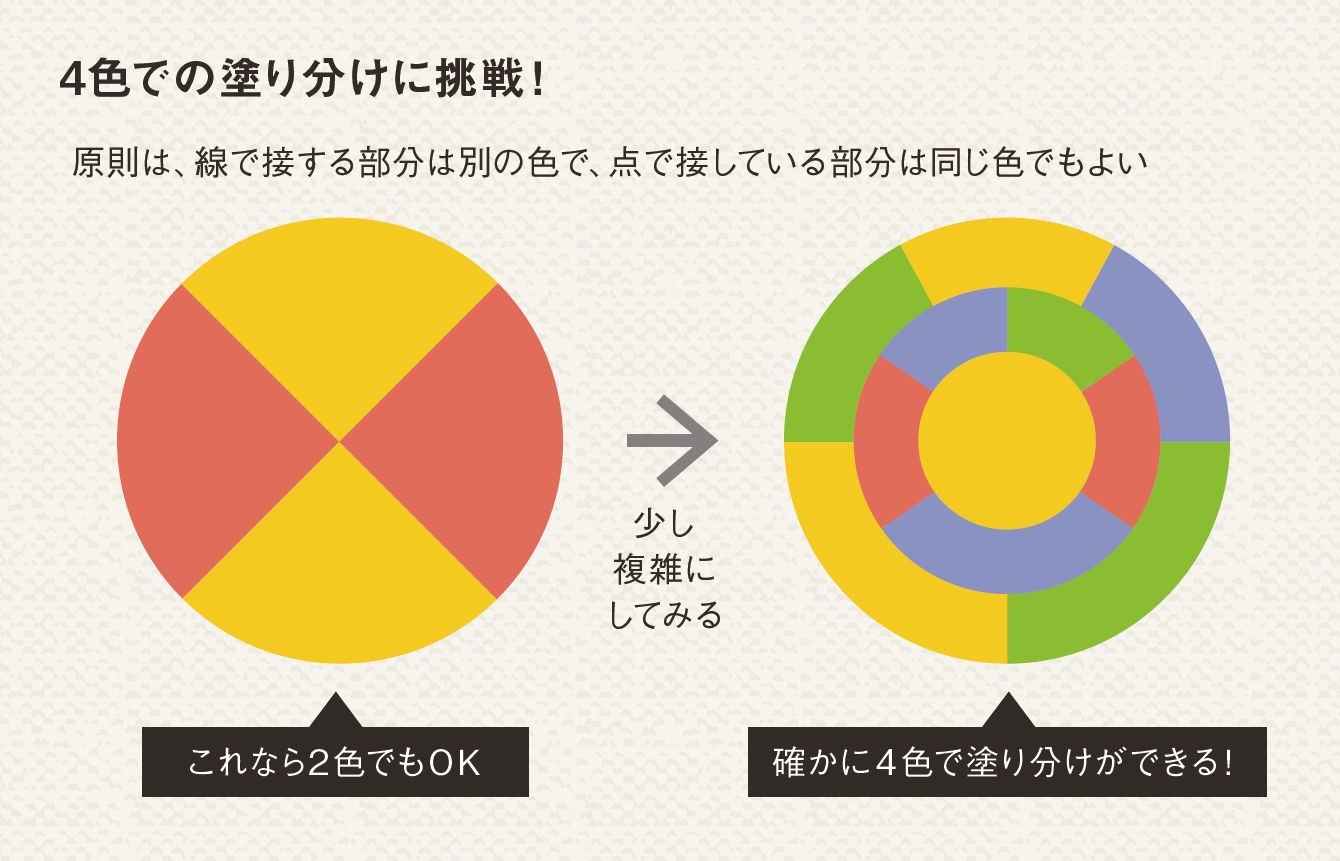
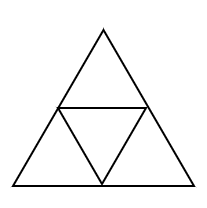
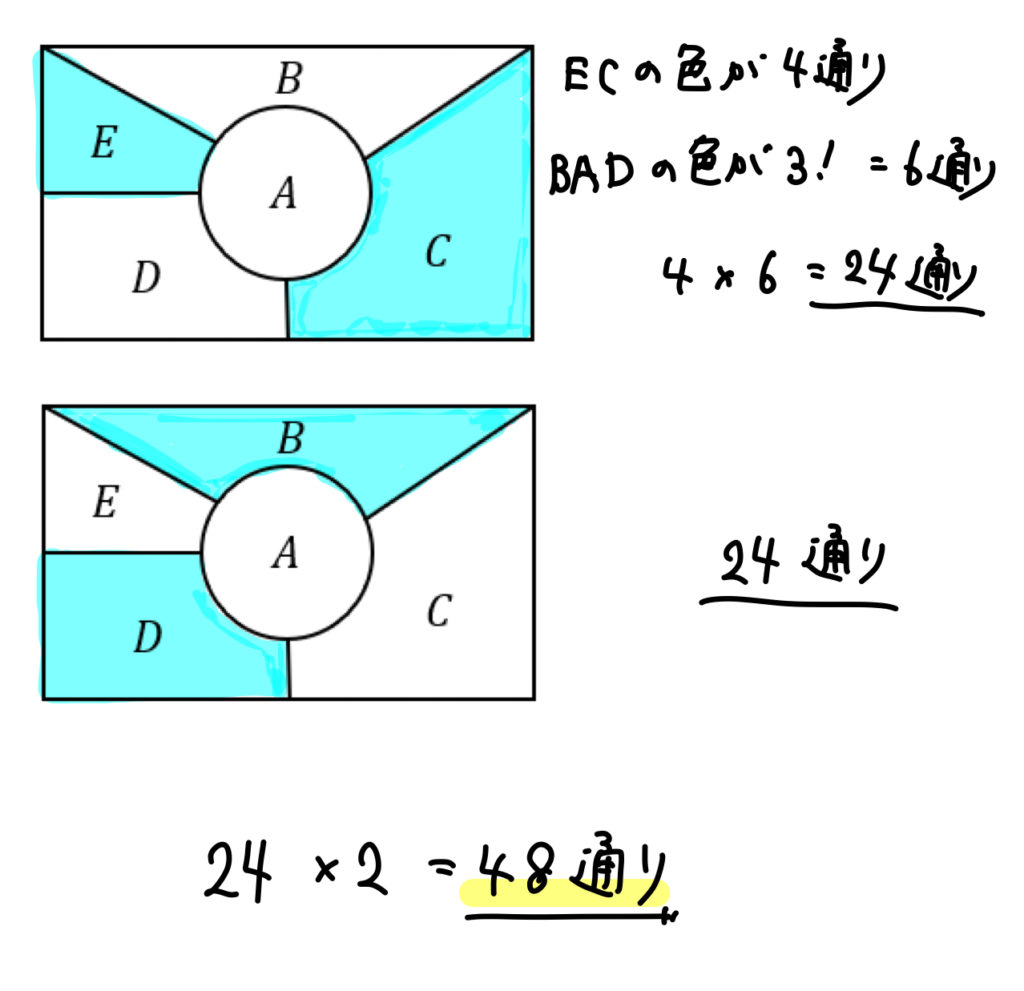
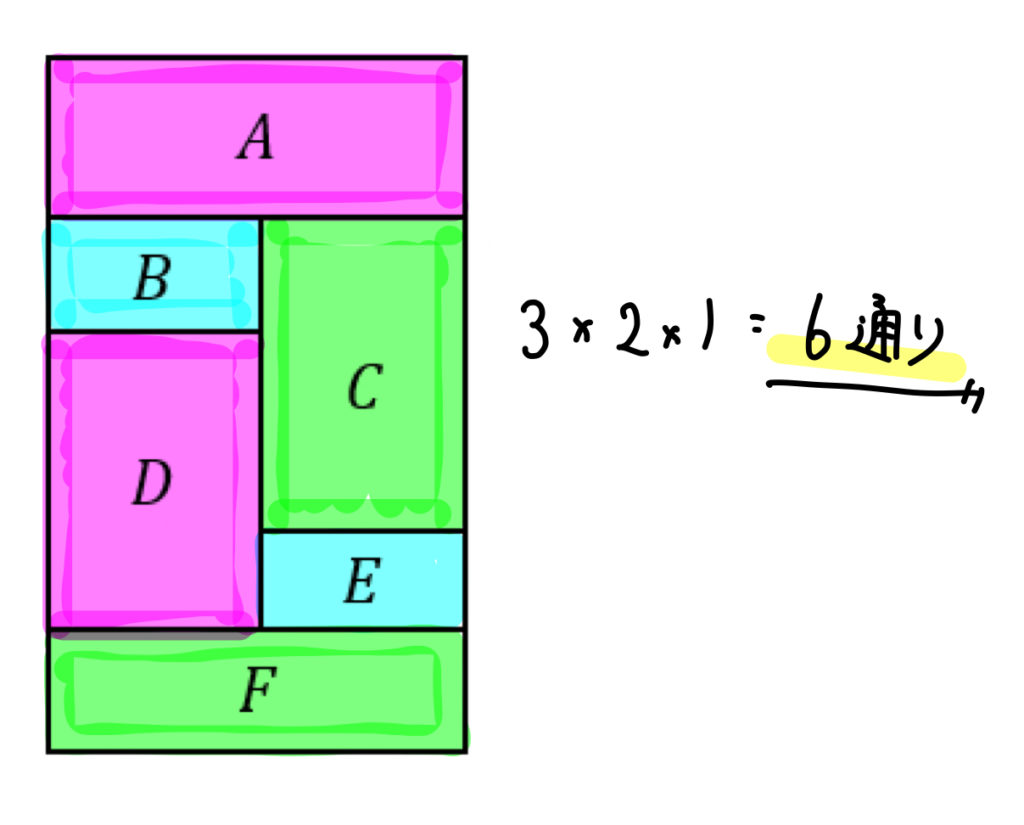
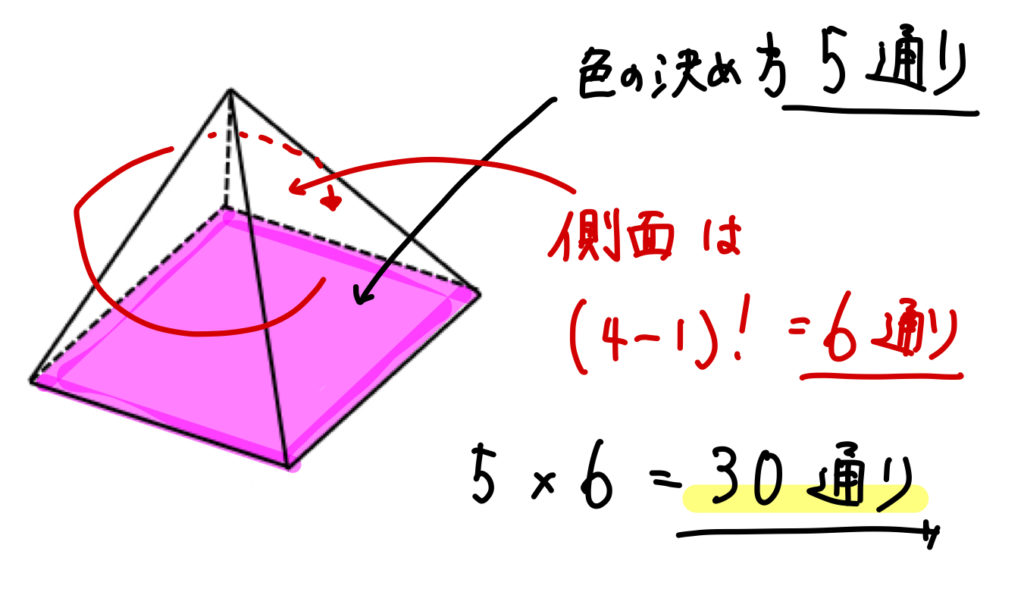
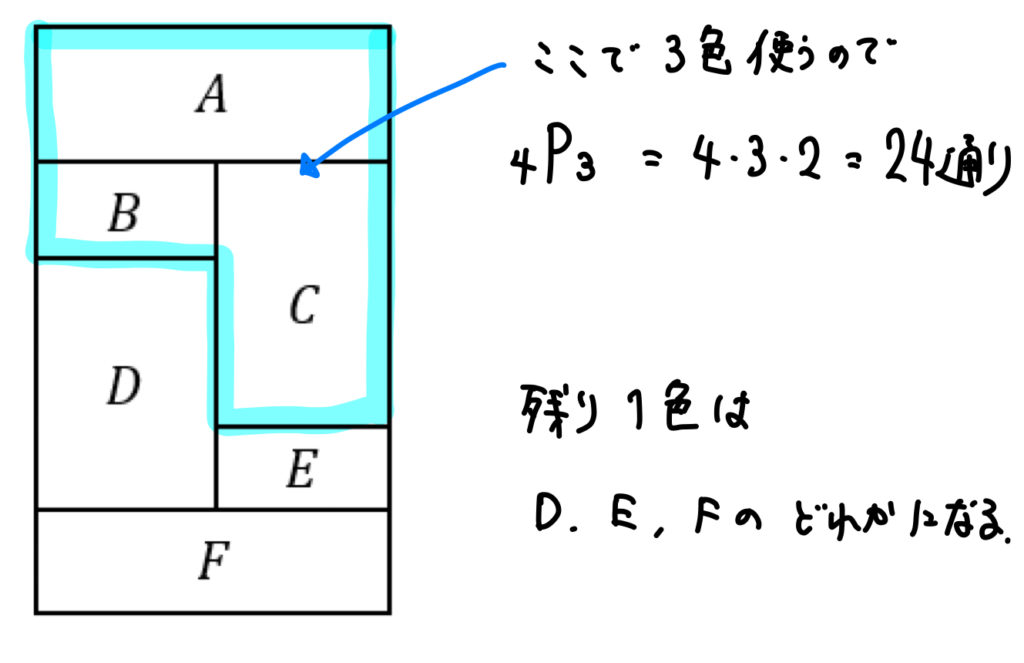
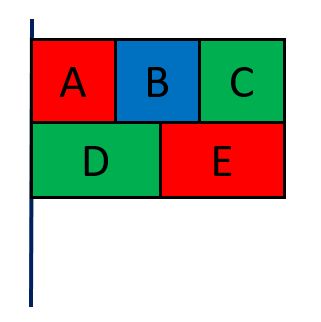
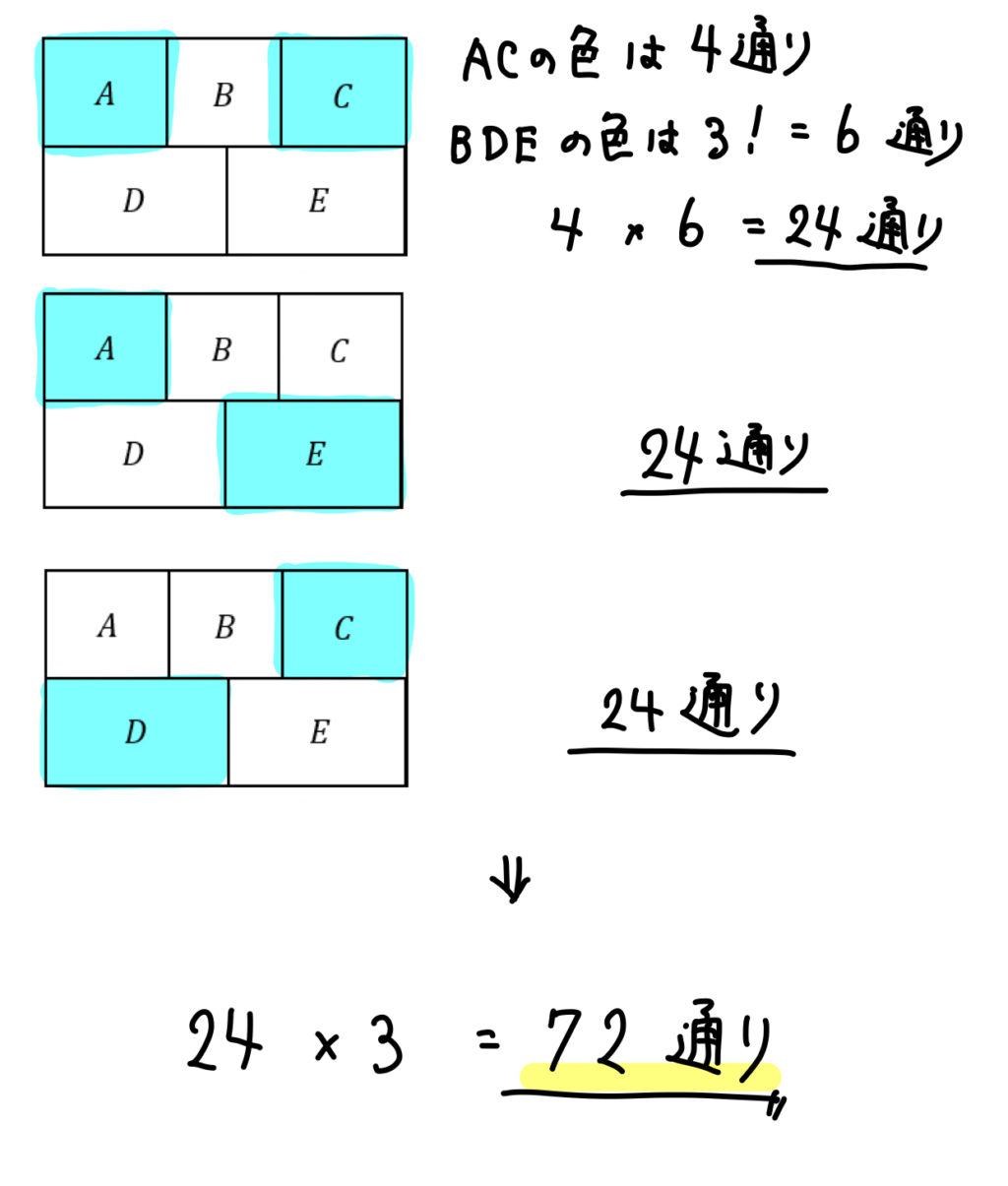
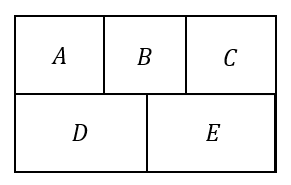
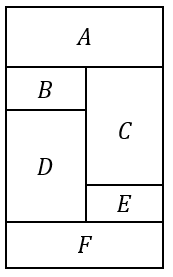
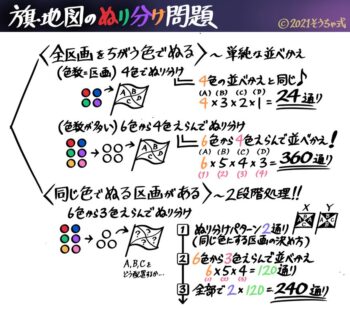
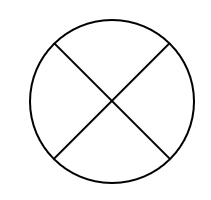
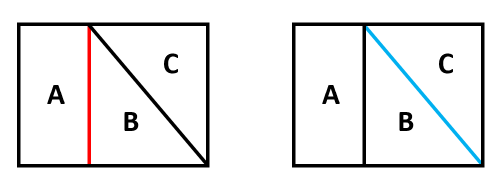
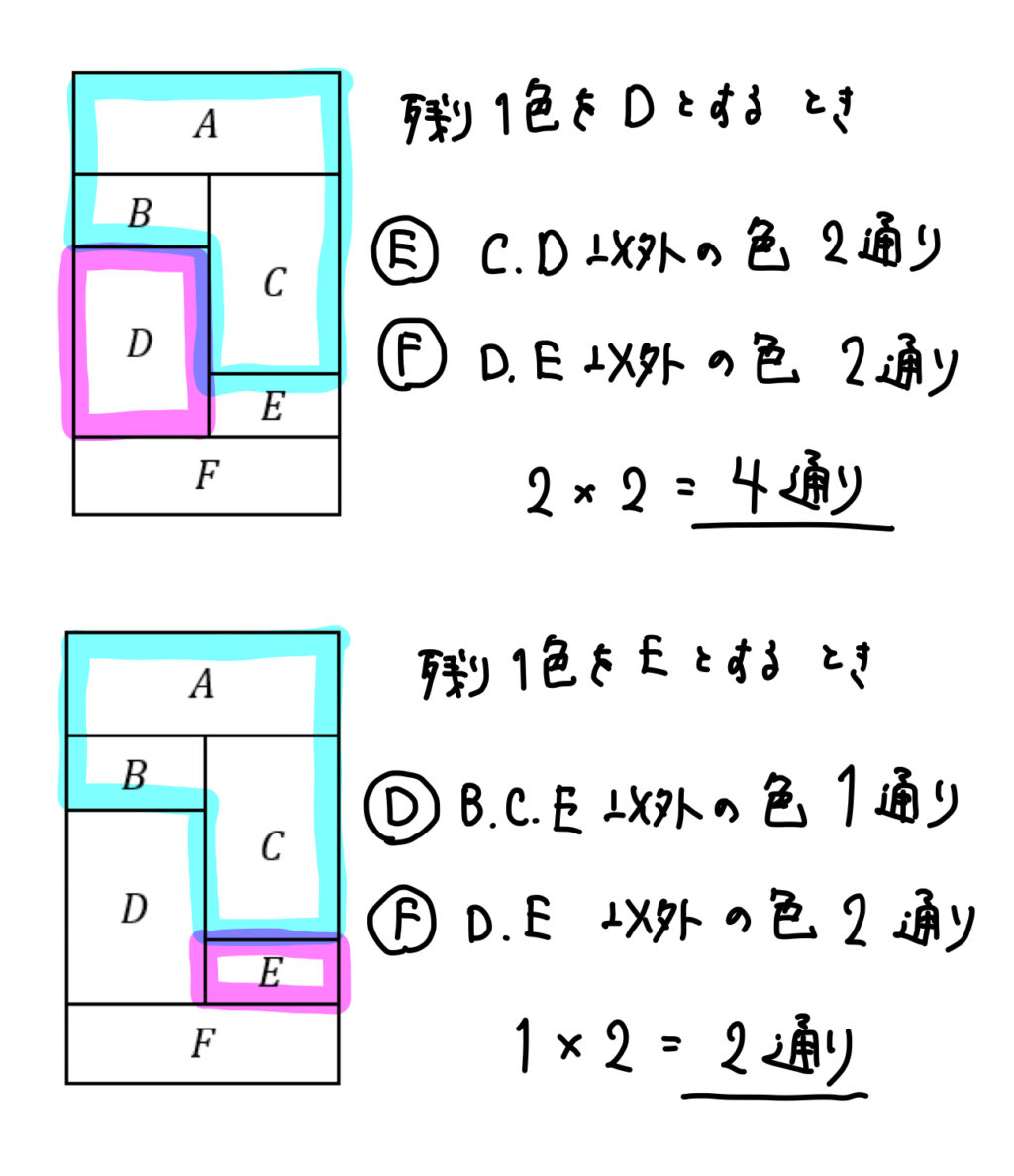
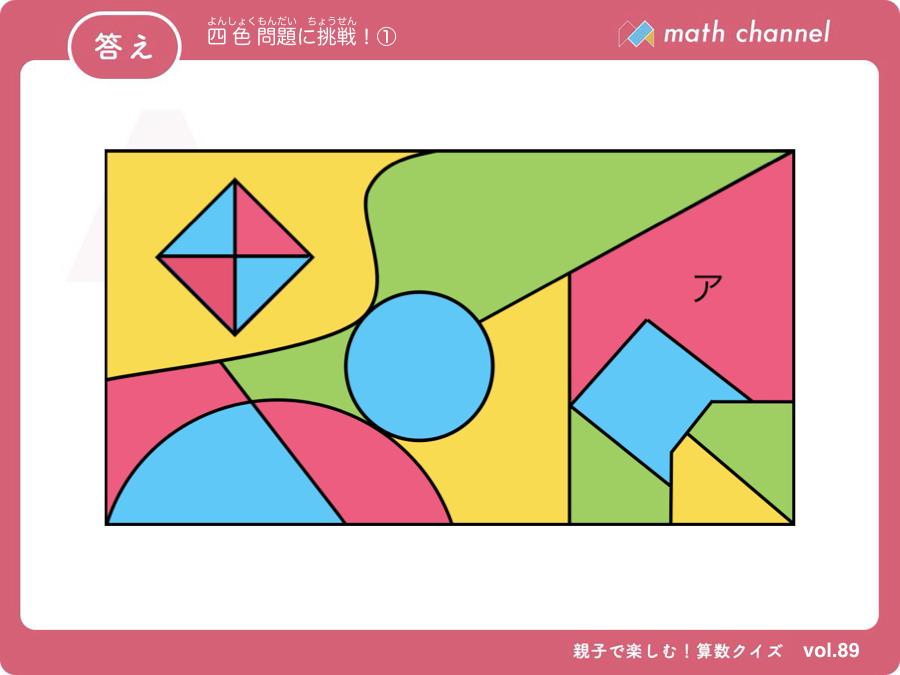
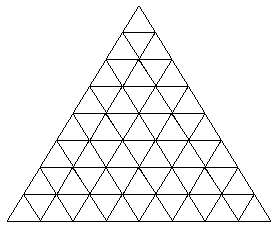
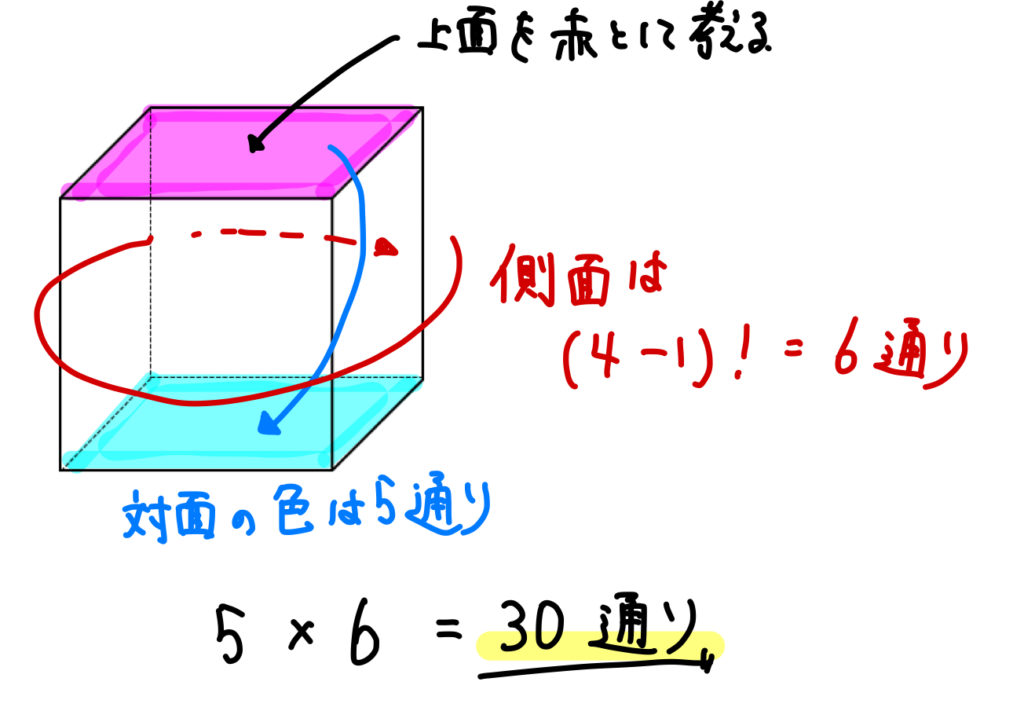
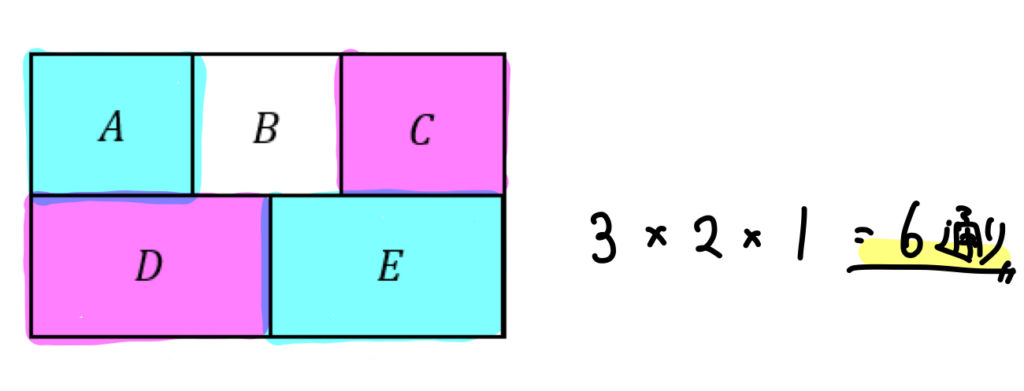
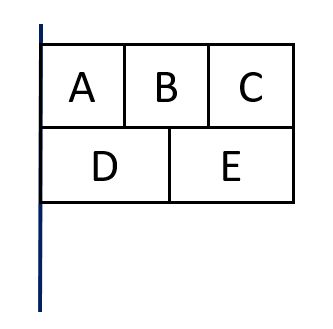
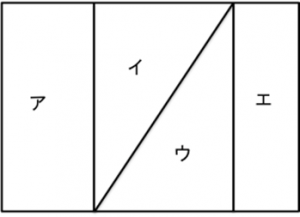
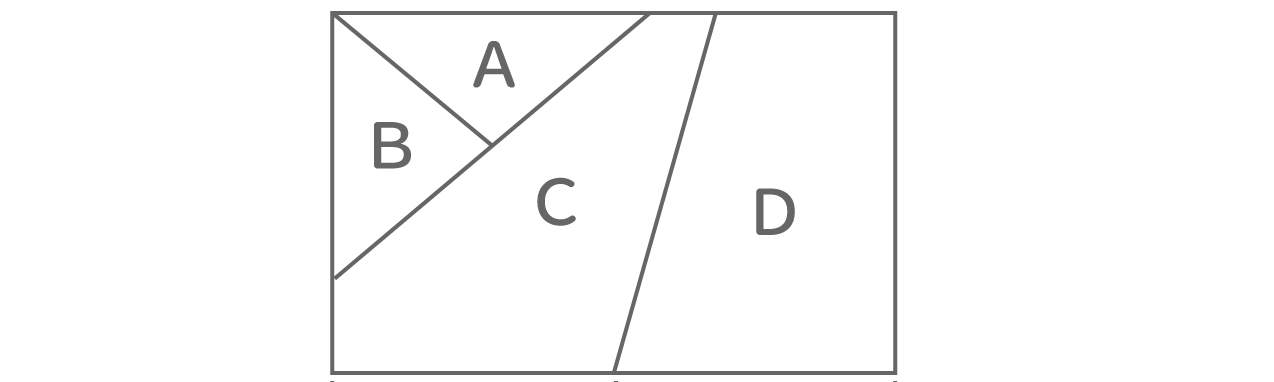
塗り分け問題 円-す。塗り分け方は全部で何通りですか。ただし、隣り合う部分は異な る色に塗るものとします。 13 次の図の5つの部分を、5色の絵の具のうち4色を使って塗り分けま す。塗り分け方は全部で何通りですか。ただし、隣り合う部分は異なこの問題は、aケーレイが1878年にロンドン数学会の席上で提起して以来、人々の注目を集めるようになった。 塗り分けが3色では不十分であることは、 1 を見れば明らかだろう。
塗り分け問題 円のギャラリー
各画像をクリックすると、ダウンロードまたは拡大表示できます
 | ||
 |  |  |
 | ||
 |  |  |
「塗り分け問題 円」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 | ||
 |  |  |
「塗り分け問題 円」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  | |
 |  | |
 |  |  |
「塗り分け問題 円」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 |  | |
 |  | |
 |  | |
「塗り分け問題 円」の画像ギャラリー、詳細は各画像をクリックしてください。
 | ||
 |  | |
 |  |  |
 |  | |
「塗り分け問題 円」の画像ギャラリー、詳細は各画像をクリックしてください。
 | ||
 |  | |
 |  |  |
「塗り分け問題 円」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 |  | |
 | ||
 |  | |
「塗り分け問題 円」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 | ||
 | ||
 |  | |
「塗り分け問題 円」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 |  |  |
問題と解説 円周上の各点と「円の中心」を結ぶことからスタートです。 難しい問題ですが、ぜひチャレンジしてください。 5年生向け 神戸女学院中学部08 平面図形 問題と解説 5年生向け 神戸女 はじめに AIREV株式会社の上里です。 以前に投稿したDiscrete Quadratic Model(DQM)で地図の塗り分け問題を解く記事で、カナダの州を4色で塗り分けてみました。 こちらはDWaveの公式ドキュメントの例題を使わせていただいたのですが、塗り分け結果の地図をまじまじ見ていると、「3色でも塗り分け
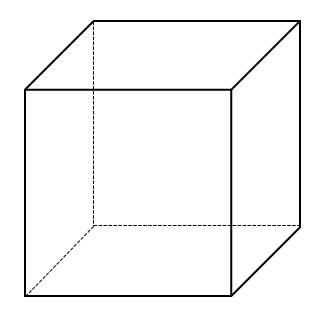
Incoming Term: 塗り分け問題, 塗り分け問題 3色, 塗り分け問題 中学受験, 塗り分け問題 円, 塗り分け問題 立方体, 塗り分け問題 4色, 塗り分け問題 立体, 塗り分け問題 3色 円, 塗り分け問題 5色, 塗り分け問題 4色以内,




0 件のコメント:
コメントを投稿